前言

自从学习C语言考进了团队之后，先是跟着学长的教程学习了一些 C++ 的基础知识。毕竟在做题方面，C++提供了很多实用的数据结构和函数，十分的方便。之后我就一直在学算法，直到今年的蓝桥杯大赛。算法这东西真是深奥的很，也很有魅力。我学的不是很快，也并不是很好，只学了一些常用的算法，记了一些模板。这期间我也打过很多的学校的算法比赛，都取得的较优异的成绩，可惜最后蓝桥杯的结果并不是很好。
但说白了学习这么久的算法又不是只为了那些奖，不管结果如何，这段时间的学习属实是给我带来了不小的收获。
首先就是我从“二指禅”的打字方法也是练到了很快的打字速度，以前还为打字慢而焦虑，现在一想都是熟能生巧，没什么好急的。再就是学习算法让我从只会C语言语法的小白真正理解并体会到了编程的含义与魅力，也让我的打下了扎实良好的编程习惯，真是收益匪浅啊。

一些算法模板

快速排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
void quick_sort(int q[], int l, int r)
{
    if (l >= r)
        return;
        
    int x = q[l], i = l - 1, j = r + 1;

     while (i < j)
     {
        while (q[++i] < x);
        while (q[--j] > x);

        if (i < j)
            swap(q[i], q[j]);
    }

    quick_sort(q, l, j);
    quick_sort(q, j + 1, r);
}

边界问题
因为边界问题只有这两种组合，不能随意搭配

1
2
// x不能取q[l]和q[l+r>>1]; 
quick_sort(q,l,i-1),quick_sort(q,i,r);
1
2
// x不能取q[r]和q[(l+r+1)>>1];
quick_sort(q,l,j),quick_sort(q,j+1,r);

归并排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
void merge_sort(int q[], int l, int r) 
{ 
    //递归的终止情况 
    if (l >= r) 
        return; 
        
    //第一步：分成子问题 
    int mid = l + r >> 1;
    
    //第二步：递归处理子问题
    merge_sort(q, l, mid); 
    merge_sort(q, mid + 1, r); 
    
    //第三步：合并子问题 
    int k = 0, i = l, j = mid + 1;
    while (i <= mid && j <= r) 
        if (q[i] <= q[j]) 
            tmp[k ++ ] = q[i ++ ]; 
        else 
            tmp[k ++ ] = q[j ++ ]; 
            
    while (i <= mid) tmp[k ++ ] = q[i ++ ]; 
    while (j <= r) tmp[k ++ ] = q[j ++ ]; 
    
    //第四步：复制回原数组 
    for (i = l, j = 0; i <= r; i ++, j ++ ) 
        q[i] = tmp[j]; }

整数二分

对lower_bound来说，它寻找的就是第一个满足条件“值大于等于x”的元素的位置；对upper_bound函 数来说，它寻找的是第一个满足“值大于 x”的元素的位置。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
bool check(int x) {/* ... */}  // 检查x是否满足某种性质 

// 区间[l, r]被划分成[l, mid]和[mid + 1, r]时使用： 
int bsearch_1(int l, int r) 
{ 
    while (l < r) 
    { 
        int mid = l + r >> 1; 
        if (check(mid)) 
            r = mid; // check()判断mid是否满足性质
        else l = mid + 1; //左加右减 
    } 
    return l; 
} 

// 区间[l, r]被划分成[l, mid - 1]和[mid, r]时使用： 
int bsearch_2(int l, int r) 
{ 
    while (l < r) 
    { 
        int mid = l + r + 1 >> 1; //如果下方else后面是l则这里加1 
        if (check(mid))
            l = mid;
        else r = mid - 1; //左加右减
    } 
    return l; 
}

浮点数二分

1
2
3
4
5
6
7
8
9
10
11
12
13
14
bool check(double x) {/* ... */} // 检查x是否满足某种性质 

double bsearch_3(double l, double r) 
{ 
    const double eps = 1e-6; 
    // eps 表示精度，取决于题目对精度的要求 
    while (r - l > eps) 
    { 
        double mid = (l + r) / 2; 
        if (check(mid)) r = mid; 
        else l = mid; 
    } 
    return l; 
}

高精度加法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
// C = A + B, A >= 0, B >= 0 
vector<int> add(vector<int> &a, vector<int> &b)
{ 
    //c为答案 
    vector<int> c; 
    //t为进位 
    int t = 0;
    for(int i = 0; i < a.size() ||i < b.size(); i ++)
    { 
        //不超过a的范围添加a[i] 
        if(i < a.size()) t += a[i]; 
        //不超过b的范围添加b[i] 
        if(i < b.size()) t += b[i]; 
        //取当前位的答案 
        c.push_back(t % 10); 
        //是否进位
        t /= 10;
    } 
    //如果t!=0的话向后添加1 
    if(t) c.push_back(1); 
    
    return c; 
}

高精度减法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
// C = A - B, 满足A >= B, A >= 0, B >= 0 
vector<int> sub(vector<int> &A, vector<int> &B) 
{ 
    //答案 
    vector<int> C; 
    //遍历最大的数 
    for (int i = 0, t = 0; i < A.size(); i ++ ) 
    { 
        //t为进位 
        t = A[i] - t; 
        //不超过B的范围t = A[i] - B[i] - t; 
        if (i < B.size()) t -= B[i]; 
        
        //合二为一，取当前位的答案
        C.push_back((t + 10) % 10);
        
        //t<0则t=1 
        if (t < 0) t = 1; 
        //t>=0则t=0 
        else t = 0; 
    } 
    
    //去除前导零 
    while (C.size() > 1 && C.back() == 0)
        C.pop_back(); 
        
    return C; 
}

高精度比大小

1
2
3
4
5
6
7
8
9
10
11
12
//高精度比大小 
bool cmp(vector<int> &A, vector<int> &B) 
{ 
    if (A.size() != B.size()) 
        return A.size() > B.size();
        
    for (int i = A.size() - 1; i >= 0; i -- ) 
        if (A[i] != B[i]) 
            return A[i] > B[i]; 
            
    return true;
}

高精度乘低精度

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
// C = A * b, A >= 0, b >= 0 
vector<int> mul(vector<int> &A, int b) 
{ 
    //类似于高精度加法 
    vector<int> C; 
    //t为进位 
    int t = 0;
    for (int i = 0; i < A.size() || t; i ++ ) 
    { 
        //不超过A的范围t=t+A[i]*b 
        if (i < A.size()) t += A[i] * b; 
        //取当前位的答案 
        C.push_back(t % 10); 
        //进位 
        t /= 10; 
    } 
    
    //去除前导零 
    while (C.size() > 1 && C.back() == 0) 
        C.pop_back(); 
        
    return C;
}

高精度乘高精度

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
vector<int> mul(vector<int> &A, vector<int> &B) 
{ 
    vector<int> C(A.size() + B.size()); 
    // 初始化为 0，C的size可以大一点 
    for (int i = 0; i < A.size(); i++) 
        for (int j = 0; j < B.size(); j++) 
            C[i + j] += A[i] * B[j]; 
            
    for (int i = 0,t = 0; i < C.size(); i++) 
    { 
        // i = C.size() - 1时 t 一定小于 10
        t += C[i]; 
        C[i] = t % 10;
        t /= 10; 
    } 
    
    while (C.size() > 1 && C.back() == 0) 
        C.pop_back(); // 必须要去前导 0，因为最高 位很可能是 0 
        
    return C; 
}

高精度除低精度

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
// A / b = C ... r, A >= 0, b > 0 
vector<int> div(vector<int> &A, int b, int &r) //高精度A，低精度b，余数r 
{ 
    vector<int> C; //答案 
    r = 0; 
    for (int i = A.size() - 1; i >= 0; i -- ) 
    { 
        r = r * 10 + A[i];
        //补全r>=b 
        C.push_back(r / b);
        //取当前位的答案 
        r %= b;
        //r%b为下一次计算 
    } 
    
    reverse(C.begin(), C.end()); //倒序为答案 
    
    while (C.size() > 1 && C.back() == 0) 
        C.pop_back(); //去除前导零 
        
    return C; 
}

高精度除高精度

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
vector<int> div(vector<int> &A, vector<int> &B, vector<int> &r) 
{ 
    vector<int> C; 
    
    if (!cmp(A, B)) 
    { 
        C.push_back(0);
        r.assign(A.begin(), A.end());
        return C; 
    } 
    
    int j = B.size();
    r.assign(A.end() - j, A.end());
    while (j <= A.size()) 
    { 
        int k = 0; 
        while (cmp(r, B)) 
        {
            r = sub(r, B);
            k ++;
        }
        
        C.push_back(k); 
        
        if (j < A.size())
            r.insert(r.begin(), A[A.size() - j - 1]);
        if (r.size() > 1 && r.back() == 0) 
            r.pop_back();
            
        j++;
    } 
    
    reverse(C.begin(), C.end());
    
    while (C.size() > 1 && C.back() == 0)
        C.pop_back();
    return C; 
}

一维前缀和

前缀和可以用于快速计算一个序列的区间和，也有很多问题里不是直接用前缀和，但是借用了前缀 和的思想。

1
2
3
预处理:s[i]=a[i]+a[i-1] 
求区间[l,r]:sum=s[r]-s[l-1] 
"前缀和数组"和"原数组"可以合二为一

应用

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
const int N = 100010; 
int a[N]; 

int main()
{ 
    int n, m;
    scanf("%d", &n); 
    
    for(int i = 1; i <= n; i ++)
        scanf("%d", &a[i]);
    for(int i = 1; i <= n; i ++)
        a[i] = a[i - 1] + a[i]; 
        
    scanf("%d", &m); 
    while(m --)
    { 
        int l, r;
        scanf("%d%d", &l, &r);
        printf("%d\n", a[r] - a[l - 1]); 
    } 
    
    return 0;
}

二维前缀和

1
2
3
计算矩阵的前缀和：s[x][y] = s[x - 1][y] + s[x][y -1] - s[x-1][y-1] + a[x][y] 
以(x1, y1)为左上角，(x2, y2)为右下角的子矩阵的和为： 
计算子矩阵的和：s = s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 -1]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
int s[1010][1010];
int n, m, q;

int main()
{ 
    scanf("%d%d%d", &n, &m, &q);
    
    for(int i = 1; i <= n; i ++)
        for(int j = 1; j <= m; j ++)
            scanf("%d", &s[i][j]); 
    for(int i = 1; i <= n; i ++)
        for(int j = 1; j <= m; j ++) 
            s[i][j] += s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1];
            
    while(q --)
    { 
        int x1, y1, x2, y2; 
        
        scanf("%d%d%d%d", &x1, &y1, &x2, &y2); 
        printf("%d\n", s[x2][y2] - s[x2][y1 - 1] - s[x1 - 1][y2] + s[x1 - 1][y1 - 1]); 
    } 
    
    return 0;
}

一维差分

差分是前缀和的逆运算，对于一个数组a，其差分数组b的每一项都是 a[i] 和前一项 a[i − 1] 的差。
注意：差分数组和原数组必须分开存放！！！！

1
给区间[l, r]中的每个数加上c：B[l] += c, B[r + 1] -= c

应用

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
int a[100010], s[100010]; 
int main()
{ 
    int n, m; 
    cin >> n >> m;
    
    for(int i = 1; i <= n; i ++)
        cin >> a[i];
        
    for(int i = 1; i <= n; i ++)
        s[i] = a[i] - a[i - 1];
    // 读入并计算差分数组
    
    while(m --)
    { 
        int l, r, c; 
        cin >> l >> r >> c;
        s[l] += c;
        s[r + 1] -= c; 
        // 在原数组中将区间[l, r]加上c
    } 
    
    for(int i = 1; i <= n; i ++)
    { 
        s[i] += s[i - 1];
        cout << s[i] << ' ';
    }
    // 给差分数组计算前缀和，就求出了原数组
    
    return 0;
}

二维差分

1
2
给以(x1, y1)为左上角，(x2, y2)为右下角的子矩阵中的所有元素加上c： 
S[x1, y1] += c, S[x2 + 1, y1] -= c, S[x1, y2 + 1] -= c, S[x2 + 1, y2 + 1] += c

应用

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
const int N = 1e3 + 10; 
int a[N][N], b[N][N];

void insert(int x1, int y1, int x2, int y2, int c) 
{
    b[x1][y1] += c;
    b[x2 + 1][y1] -= c; 
    b[x1][y2 + 1] -= c; 
    b[x2 + 1][y2 + 1] += c;
}

int main()
{ 
    int n, m, q;
    cin >> n >> m >> q;
    
    for (int i = 1; i <= n; i++) 
        for (int j = 1; j <= m; j++)
            cin >> a[i][j];
            
    for (int i = 1; i <= n; i++) 
    {
        for (int j = 1; j <= m; j++)
        {
            insert(i, j, i, j, a[i][j]); //构建差分数组
        }
    } 
    
    while (q --)
    {
        int x1, y1, x2, y2, c;
        cin >> x1 >> y1 >> x2 >> y2 >> c;
        insert(x1, y1, x2, y2, c); //加c
    }
    
    for (int i = 1; i <= n; i++) 
    {
        for (int j = 1; j <= m; j++)
        {
            b[i][j] += b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1]; //二维前缀和 
        } 
    } 
    
    for (int i = 1; i <= n; i++) 
    { 
        for (int j = 1; j <= m; j++) 
        {
            printf("%d ", b[i][j]);
        } 
        printf("\n");
    } 
    
    return 0;
}

位运算

1
2
求n的第k位数字: n >> k & 1 
返回n的最后一位1：lowbit(n) = n & -n

双指针

1
2
3
4
5
6
7
8
9
for (int i = 0, j = 0; i < n; i ++ ) 
{
    while (j < i && check(i, j)) j ++ ; 
    // 具体问题的逻辑
}

常见问题分类：
    (1) 对于一个序列，用两个指针维护一段区间
    (2) 对于两个序列，维护某种次序，比如归并排序中合并两个有序序列的操作

离散化

离散化的本质是建立了一段数列到自然数之间的映射关系（value -> index)，通过建立新索引，来缩 小目标区间，使得可以进行一系列连续数组可以进行的操作比如二分，前缀和等…

离散化首先需要排序去重：

  1. 排序：sort(alls.begin(),alls.end())
  2. 去重：alls.earse(unique(alls.begin(),alls.end()),alls.end())
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
vector<int> alls; // 存储所有待离散化的值
sort(alls.begin(), alls.end()); // 将所有值排序
alls.erase(unique(alls.begin(), alls.end()), alls.end()); // 去掉重复元素

// 二分求出x对应的离散化的值
int find(int x) // 找到第一个大于等于x的位置 
{ 
    int l = 0, r = alls.size() - 1; 
    while (l < r) 
    { 
        int mid = l + r >> 1;
        if (alls[mid] >= x)
            r = mid; 
        else l = mid + 1;
    } 
    
    return r + 1; // 映射到1, 2, ...n
}

应用

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
typedef pair<int, int> PII;

const int N = 300010;
int n, m;
int a[N], s[N]; 

vector<int> alls; //存入下标容器
vector<PII> add, query; //add增加容器，存入对应下标和增加的值的大小 

//query存入需要计算下标区间和的容器 
int find(int x)
{ 
    int l = 0, r = alls.size() - 1;
    while (l < r) //查找大于等于x的最小的值的下标
    {
        int mid = l + r >> 1; 
        if (alls[mid] >= x) r = mid;
        else l = mid + 1;
    } 
    
    return r + 1; //因为使用前缀和，其下标要+1可以不考虑边界问题
}

int main() 
{
    cin >> n >> m;
    
    for (int i = 0; i < n; i ++ ) 
    {
        int x, c; cin >> x >> c;
        add.push_back({x, c}); //存入下标即对应的数值c
        alls.push_back(x); //存入数组下标x=add.first
    }
    
    for (int i = 0; i < m; i ++ ) 
    { 
        int l, r; cin >> l >> r;
        query.push_back({l, r}); //存入要求的区间
        alls.push_back(l); //存入区间左右下标 
        alls.push_back(r); 
    } 
    
    // 区间去重 
    sort(alls.begin(), alls.end()); 
    alls.erase(unique(alls.begin(), alls.end()), alls.end()); // 处理插入
    
    for (auto item : add) 
    { 
        int x = find(item.first); //将add容器的add.secend值存入数组a[]当中，
        a[x] += item.second; //在去重之后的下标集合alls内寻找对应的下标并添加数值 
    } 
    
    // 预处理前缀和
    for (int i = 1; i <= alls.size(); i ++ )
        s[i] = s[i - 1] + a[i]; 
        
    // 处理询问
    for (auto item : query) 
    { 
        int l = find(item.first), r = find(item.second); //在下标容器中查找对应的左右 两端[l~r]下标，然后通过下标得到前缀和相减再得到区间a[l~r]的和
        cout << s[r] - s[l - 1] << endl;
    }
    
    return 0;
}

区间合并

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
// 将所有存在交集的区间合并
void merge(vector<PII> &segs) 
{
    vector<PII> res;
    
    sort(segs.begin(), segs.end());
    
    int st = -2e9, ed = -2e9;
    for (auto seg : segs) 
        if (ed < seg.first) 
        {
            if (st != -2e9) 
                res.push_back({st, ed});
            st = seg.first, ed = seg.second;
        } 
        else 
            ed = max(ed, seg.second);
            
    if (st != -2e9) 
        res.push_back({st, ed});
        
    segs = res;
}

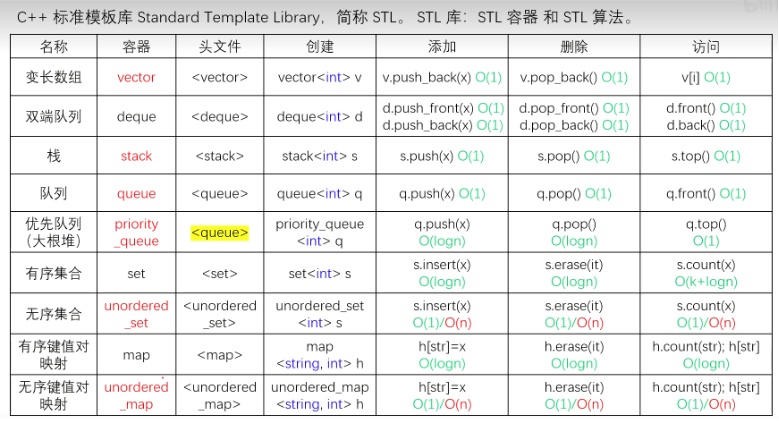
C++ STL

stl

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
vector, 变长数组，倍增的思想
    size() 返回元素个数
    empty() 返回是否为空 
    clear() 清空 
    front()/back()
    push_back()/pop_back() 
    begin()/end()
    []
    支持比较运算，按字典序
    
pair<int, int>
    first, 第一个元素 
    second, 第二个元素
    支持比较运算，以first为第一关键字，以second为第二关键字（字典序）
    
string，字符串 
    size()/length() 返回字符串长度
    empty()
    clear() 
    substr(起始下标，(子串长度)) 返回子串
    c_str() 返回字符串所在字符数组的起始地址 
    
queue, 队列
    size()
    empty() 
    push() 向队尾插入一个元素
    front() 返回队头元素
    back() 返回队尾元素
    pop() 弹出队头元素 
    
priority_queue, 优先队列，默认是大根堆
    size() 
    empty()
    push() 插入一个元素
    top() 返回堆顶元素
    pop() 弹出堆顶元素 
    定义成小根堆的方式：priority_queue<int, vector<int>, greater<int>> q;
    
stack, 栈
    size()
    empty()
    push() 向栈顶插入一个元素 
    top() 返回栈顶元素
    pop() 弹出栈顶元素
    
deque, 双端队列 
    size()
    empty() 
    clear()
    front()/back()
    push_back()/pop_back() 
    push_front()/pop_front()
    begin()/end()
    [] 
    
set, map, multiset, multimap, 基于平衡二叉树（红黑树），动态维护有序序列 
    size() 
    empty()
    clear() 
    begin()/end() 
    ++, -- 返回前驱和后继，时间复杂度 O(logn)
    
    set/multiset insert() 插入一个数 
        find() 查找一个数 
        count() 返回某一个数的个数
        erase()
            (1) 输入是一个数x，删除所有x O(k + logn) 
            (2) 输入一个迭代器，删除这个迭代器
        lower_bound()/upper_bound()
            lower_bound(x) 返回大于等于x的最小的数的迭代器
            upper_bound(x) 返回大于x的最小的数的迭代器 
            
    map/multimap 
        insert() 插入的数是一个pair
        erase() 输入的参数是pair或者迭代器 
        find() 
        [] 注意multimap不支持此操作。 时间复杂度是 O(logn)      
        lower_bound()/upper_bound()
        
unordered_set, unordered_map, unordered_multiset, unordered_multimap, 哈希表 
    和上面类似，增删改查的时间复杂度是 O(1)
    不支持 lower_bound()/upper_bound()， 迭代器的++，-- 

bitset, 圧位 
    bitset<10000> s;
    ~, &, |, ^ 
    >>, << ==, != 
    [] 
    
    count() 返回有多少个1 
    
    any() 判断是否至少有一个1 
    none() 判断是否全为0 
    
    set() 把所有位置成1 
    set(k, v) 将第k位变成v 
    reset() 把所有位变成0 
    flip() 等价于~ 
    flip(k) 把第k位取反

DFS

1
2
3
4
5
6
7
8
9
10
int dfs(int u) 
{ 
    st[u] = true; // st[u] 表示点u已经被遍历过 
    
    for (int i = h[u]; i != -1; i = ne[i])
    { 
        int j = e[i]; 
        if (!st[j]) dfs(j); 
    } 
}

应用：数字全排列、树的重心、n-皇后等。

BFS

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
queue<int> q; st[1] = true; // 表示1号点已经被遍历过
q.push(1); 

while (q.size())
{ 
    int t = q.front();
    q.pop();
    for (int i = h[t]; i != -1; i = ne[i]) 
    { 
        int j = e[i];
        if (!st[j])
        {
            st[j] = true; // 表示点j已经被遍历过
            q.push(j);
        }
    }
}

应用：走迷宫、八数码等。

动态规划

这里只学了背包

01背包每件物品只能装一次
完全背包每件物品可以装无限次
多重背包每件物品只能装有限次（多次）
分组背包每组只能选择一件物品装入（01背包升级）

01背包

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
const int N = 1010; 
int n, m; 
int v[N], w[N]; //v代表体积，w代表价值 
int f[N][N]; 

int main()
{ 
    cin >> n >> m; 
    for(int i = 1; i <= n; i ++)
        cin >> v[i] >> w[i]; 
        
    for(int i = 1; i <= n; i ++) //i代表这n件物品 
    { 
        for(int j = 1; j <= m; j ++) //j代表背包容量
        { 
            if(v[i] > j) //如果v[i]的容量大于当前的背包容量则不装进行下一个 
                f[i][j] = f[i - 1][j]; 
            else 
                f[i][j] = max(f[i - 1][j],f[i - 1][j - v[i]] + w[i]); //如果v[i]的容量小于当 前背包容量则可以选择装与不装得到最大值 
        } 
    } 
    
    cout << f[n][m] << endl; //输出最后的一个一定是最大的 
    return 0; 
}

01背包，使用滚动数组，倒序遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
const int N = 1010; 
int n, m; 
int v[N], w[N]; //v代表体积，w代表价值 
int dp[N]; 

int main()
{ 
    cin >> n >> m; 
    for(int i = 1; i <= n; i ++) //i代表这n件物品 
    { 
        cin >> v[i] >> w[i]; //在线算法 
        for(int j = m; j >= v[i]; j --) //j代表背包容量，滚动数组必须倒序遍历
        { 
            dp[j] = max(dp[j], dp[j - v[i]] + w[i]); //滚动数组 
        } 
    } 
    
    cout << dp[m] << endl; //输出最后的一个一定是最大的 
    return 0; 
}

状态转移方程：dp[j] = max(dp[j], dp[j - v[i]] + w[i])

完全背包

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
int v[N], w[N]; 
int dp[N]; 

int main()
{ 
    int n, m; 
    cin >> n >> m; 
    for(int i = 1; i <= n; i ++) //遍历物品
    { 
        cin >> v[i] >> w[i]; //在线算法 
        for(int j = v[i]; j <= m; j ++) //正序遍历背包容量
        { 
            dp[j] = max(dp[j], dp[j - v[i]] + w[i]); //滚动数组 
        } 
    } 
    
    cout << dp[m] << endl; //输出答案 
    
    return 0; 
}

完全背包问题和01背包优化版的区别在于第二重循环的 v[i] 和m做交换
状态转移方程：dp[j] = max(dp[j], dp[j - v[i]] + w[i])

多重背包

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
int n, m;
int v[N], w[N], s[N]; 
int dp[N][N]; 

int main()
{ 
    cin >> n >> m; 
    
    for(int i = 1; i <= n; i ++)
        cin >> v[i] > >w[i] >> s[i]; 
        
    for(int i = 1; i < =n; i ++) //物品 
        for(int j = 0; j <= m; j ++) //背包容量 
            for(int k = 0; k <= s[i] && k * v[i] <= j; k ++) 
                dp[i][j] = max(dp[i][j], dp[i - 1][j - v[i] * k] + w[i] * k); 
                
    cout << dp[n][m] << endl; 
    
    return 0; 
}

状态转移方程：dp[i][j] = max(dp[i][j], dp[i - 1][j - v[i] * k] + w[i] * k) k为第i个物品的个数

分组背包

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
const int N = 110; 
int f[N]; 
int v[N][N], w[N][N], s[N];
int n, m ,k; 

int main()
{ 
    cin >> n >> m; 
    
    for(int i = 0; i < n; i ++)
    { 
        cin >> s[i];
        for(int j = 0; j < s[i]; j ++)
        { 
            cin >> v[i][j] >> w[i][j]; 
        } 
    } 
    
    for(int i = 0; i < n; i ++)
    { 
        for(int j = m; j >= 0; j --)
        { 
            for(int k = 0; k < s[i]; k ++) //for(int k=s[i];k>=1;k--)也可以 
            {
                if(j >= v[i][k]) 
                f[j] = max(f[j], f[j - v[i][k]] + w[i][k]); 
            } 
        } 
    } 
    
    cout << f[m] << endl; 
}

状态转移方程：f[j] = max(f[j], f[j - v[i][k]] + w[i][k])

—end—